Python实践投资组合理论

搞了一段时间的量化，还是个萌新，也塞进了很多统计学的术语。现做一个小小的实践验证投资组合原理。其中股票历史价格的获取来源于tushare，期待着它能加入港股，美股啥的，A股可真是个韭菜养殖场。

  1. 获取数据

我随便挑了几支股票（其实并不是，第一次选的5支股票最后的最大Sharpe Ratio是负的🌚），他们分别是：000413 东旭光电,300033 同花顺, 002007 兰华生物, 000001 平安银行, 000002 万科 A。可惜的是tushare不支持同时获取多只股票，只好用个list，再循环获取了。

1
2
3
4
5
6
7
8
9
10
stock_set = ['000413','300033','002007','000001','000002']
noa = len(stock_set)
df = pds.DataFrame()
for stock in stock_set:
    data = ts.get_h_data(stock, start='2017-01-01', end='2017-12-31')['close']
    df.insert(0,stock,data)
#数据按照日期升序排列
df=df.sort_index(ascending=True)
#规范化时序数据
(df/df.iloc[0]*100).plot()

规范化后的时间序列数据: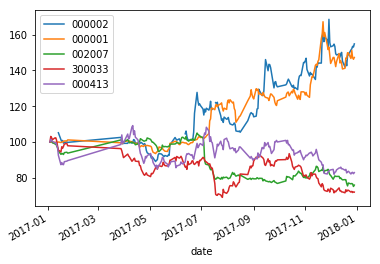
price

  1. 计算不同证券的均值、协方差

    均值-方差是指不同证券(对数)收益的均值和方差，可以这样计算
1
2
3
rets = np.log(df / df.shift(1))
#均值。我们使用252个交易日，从每日收益得出年化收益
rets.mean()*252

pandas有一个内建方法，可以生成协方差矩阵：

1
rets.cov()*252

  1. 给不同资产随机分配初始权重

下面的代码将生成5个处于(0,1)之间的随机数，然后对这些数值规范化，使所有值的总和为1：

1
2
weights = np.random.random(len(stock_set))
weights /= np.sum(weights)

  1. 计算预期组合年化收益、组合方差和组合标准差

1
2
3
pro = np.sum(rets.mean()*weights)*252#预期组合年化收益
var = np.dot(weights.T,np.dot(rets.cov()*252),weights)#预期组合方差
stand_var = np.sqrt(var)#预期组合标准差

var的公式转换为Python numpy的向量化并没有那么容易理解。首先你得明白组合方差的计算方法，此处给个B站传送门投资组合预期收益和收益方差计算,这么棒的视频当然要滋词滋词。

  1. 用蒙特卡洛模拟产生大量随机组合

采用蒙特卡洛模拟生成较大规模的随机投资组合权重。然后选出最优权重。对于每一次的模拟，我们都记录得出的预期投资组合的均值和方差：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
port_returns = []
port_variance = []
for p in range(4000):
    weights = np.random.random(len(stock_set))
    weights /=np.sum(weights)
    port_returns.append(np.sum(returns.mean()*252*weights))
    port_variance.append(np.sqrt(np.dot(weights.T, np.dot(returns.cov()*252, weights))))

port_returns = np.array(port_returns)
port_variance = np.array(port_variance)

#无风险利率设定为4%
risk_free = 0.04
plt.scatter(port_variance, port_returns, c=(port_returns-risk_free)/port_variance)
plt.grid(True)
plt.xlabel('excepted volatility')
plt.ylabel('expected return')
plt.colorbar(label = 'Sharpe Ratio')

结果展示：
montecarlo

Comments

⬆︎TOP