Java实现DFS和BFS

包括了无向无权图的邻接表构造，和对图的深度优先遍历以及广度优先遍历。讲真，Java是真心不方便啊，python多快鸭。

图的构造

我打算用图存各种人名，人际关系网络的初步实现。然后为了方便判断人名在遍历时是否已经访问过，我索性建立图的最小单位Node,类实现如下：

1
2
3
4
5
6
7
8
9
10
11
public class Node {
 
	private String name;		// 存储人名
	private boolean marked; // 标记信息
	
	public Node(String name){
	    this.name = name;
	    marked = false;
	}
	/******** getter and setter ********/
}

使用邻接表(Adjacent List)实现对图的表示，而邻接表用Map<Node,List<Node>>实现，map的键是图中的节点，键对应的值是与该节点邻接的所有节点，存放在List<Node>中。图的类属性和构造方法如下所示：

1
2
3
4
5
6
7
8
9
10
11
public class G {
    private int vertex;	// 定点数
    private int egde;	// 边数

    private Map<Node,List<Node>> adj;    // 邻接表
    public G(){
        vertex = 0;
        egde = 0;
        adj = new HashMap<>();
    }
}

上述代码能够通过构造函数构造没有节点的空图。所以在给他添上 addEdge(Node,Node)方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public void addEdge(Node Node_1, Node Node_2){
	// 给Node_1添加相邻节点
    if (adj.containsKey(Node_1)) {
        adj.get(Node_1).add(Node_2);
    }
    else {
        List<Node> l = new LinkedList<>();
        l.add(Node_2);
        adj.put(Node_1,l);
    }
// 给Node_2添加相邻节点
    if (adj.containsKey(Node_2)) {
        adj.get(Node_2).add(Node_1);
    }
    else {
        List<Node> l = new LinkedList<>();
        l.add(Node_1);
        adj.put(Node_2,l);
    }

    vertex = adj.size();
    egde ++;
}

例如，在调用addEdge(n1,n2)方法时，会在邻接表的键为n1对应的值中添加n2,同样也会在键为n2对应的值中添加n1。

为了使用BFS或者DFS,图必须还提供一个 返回某个特定节点的所有相邻节点，这个好实现：

1
2
3
public List<Node> getAdj(Node n){
    return adj.get(n);
}

好了，图类就写好了。

BFS

BFS的思想就是利用队列存储节点的相邻节点。比方说我有个图如下图所示：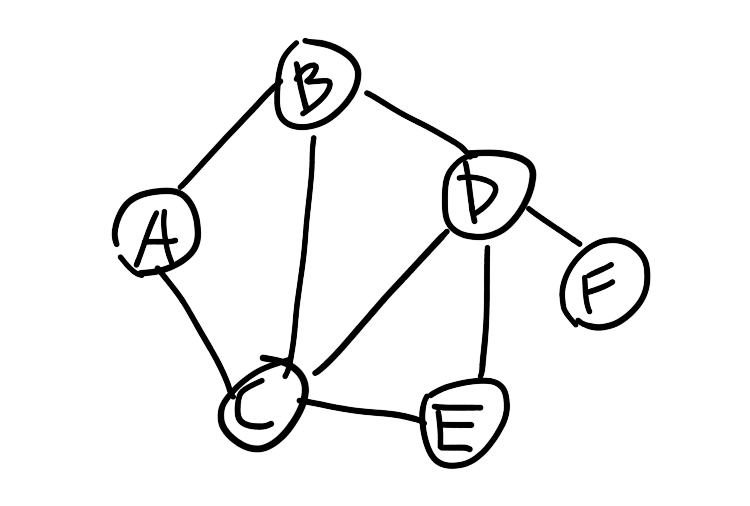
G

如果我们滴起始节点设为’A’，那么该思想就是意味着：把’A’放入队列，当队列不为空时，队列的队首元素(此时是A)出队列，然后将该元素(此时是A)的 相邻节点:’B’、’C’放入队列，重复上述步骤即可或得BFS结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Queue<Node> queue = new LinkedList<>();
queue.offer(A);
A.setMarked(true);

while(!queue.isEmpty()){
    Node o = queue.poll();
    System.out.print(o.getName()+"\t");

    List<Node> list = g.getAdj(o);
    for (Node n : list) {
        if (!n.isMarked()) {
            // 如果没有被访问过
            queue.add(n);
            // 访问标志位改为true表示已经被访问了
            n.setMarked(true);
        }
    }
}

BFS除了有遍历图的功能，它也是图最短路径的基础。因为，BFS是一层一层遍历的，如图：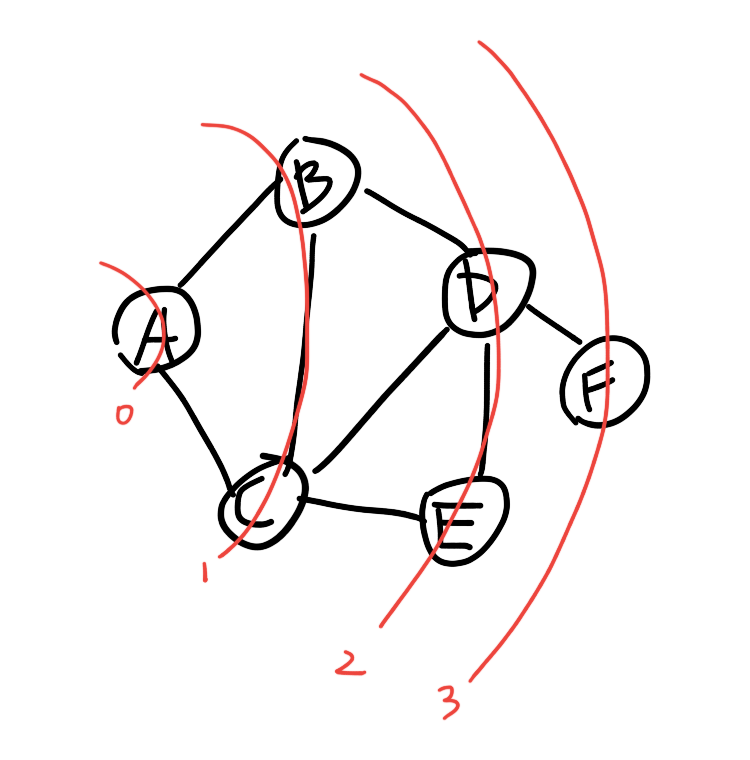
BFS

每一圈红色的曲线上的点到A的距离是相同的，就像水面的涟漪一样。但是，举个例子，想要知道A->D的路径经过了哪些节点，那么得在BFS遍历时额外存储的某个节点的上一个节点，如B->A,C->A,D->B,E->C,F->D，这些信息存储起来，那么A->D的路劲怎么求呢？，由于A->D的路劲等同于D->A，而D->A = D->B->A，从而解决了路径问题。

DFS

DFS的思想就是利用栈存储节点的相邻节点，可见，将队列换成栈，即可实现BFS到DFS的转换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Stack<Node> stack = new Stack<>();
stack.push(A); //把A入栈
A.setMarked(true);  // 并且把A的访问标记设置为true，防止重复

while(!stack.isEmpty()){
    Node o = stack.pop();

    System.out.print(o.getName()+"\t");

    List<Node> list = g.getAdj(o);
    for (Node n : list) {
        if (!n.isMarked()) {
            // 没有被访问过
            stack.push(n);
            n.setMarked(true);
        }
    }
}

Comments

⬆︎TOP