浮点数的二进制表示

在金融公司实习时遇到大数字浮点数是常有的事情，可这数字准确度可不能含糊，哪怕是小数最后一位少了，那也是不能接受的，毕竟都是💰嘛。Java.math包下的大数类可以解决float、double精度丢失的问题。计组教材其实有详细的介绍浮点数的二进制存储,奈何计组学的不怎么地，因此今日就重新温（预）习一波。

float,double类型的二进制表示

我们先来看看java中,double类型数据的二进制存储值，和展示的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public class IEEE754 {

    /* ieee 754 双精度常量 */
    private static final int NOR_LEN_64 = 64;
    private static final int M_LEN_64 = 52;
    private static final int E_LEN_64 = 11;

    /* ieee 754单精度常量*/
    private static final int NOR_LEN_32 = 32;
    private static final int M_LEN_32 = 23;
    private static final int E_LEN_32 = 8;


    public static void main(String[] args) {
        printBit(2.5);
    }

    private static void printBit(double d) {
        System.out.println("##"+d);
        long l = Double.doubleToLongBits(d);
        String bits = Long.toBinaryString(l);
        int len = bits.length();
        System.out.println(bits+"#"+len);

        if (len != NOR_LEN_64){// 正数长度为63，最高位默认为0
            bits = "0" + bits;
        }
        System.out.println("S[63]"+bits.charAt(0));
        System.out.println("E[62-52]"+bits.substring(1,1+E_LEN_64));
        System.out.println("M[51-0]"+bits.substring(NOR_LEN_64-M_LEN_64,NOR_LEN_64));
    }
}

输入如下：

1
2
3
4
5
##2.5
100000000000100000000000000000000000000000000000000000000000000#63
S[63]0
E[62-52]10000000000
M[51-0]0100000000000000000000000000000000000000000000000000

你可能会疑惑，用S\E\M分割2.5在计算机中存储的二进制有什么意义呢？计算机又是怎么把2.5编程01的呢？答案就是IEEE754，它定义了系列规则标准。

IEEE754

那我们就从2.5入手，窥探IEEE754的秘密。

1.把2.5(10)转成二进制（使用乘二取整的方法）

1
2.5(10) = 10.1(2)

2. 转成1.xxx 2^y的形式或者 0.xxx2^y的形式

你可能会疑惑，第一步能理解为什么，这一步就直接懵逼了。别怕，这就是规定罢了。你也可以简单的理解为用科学计数法的形式标准化表示小数形式的二进制，

1
10.1(2) = 1.01 * 2 ^ 1

3. 对应S、E、M

根据国际标准IEEE 754，任意一个二进制浮点数V可以表示成下面的形式：

V = (-1)^S × M × 2^E
其中：
S是符号位，0正，1负
M是有效位，1<=M<2（规约形式）或者,0<=M<1（非规约形式,绝对值小于1的数）
2^E 表示指数位

单精度浮点数在计算机中占了32位（4个字节），32位中分成了不同的区间，其中第[31]为是Sign符号位，[30-23]是Exponent指数位，[22-0]是有效位，也可以叫小数位Fraction。

双精度浮点数在计算机中占了64位（8个字节），64位中分成了不同的区间，其中第[63]为是Sign符号位，[62-52]是Exponent指数位，[51-0]是有效位，也可以叫小数位Fraction。


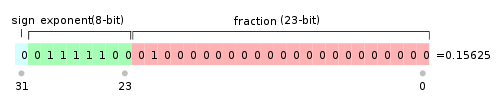
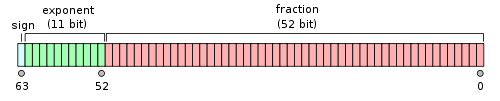
所以，(-1)^0 × 1.01 × 2^1 对应分别是：

S=0
M=1.01
E=1

4.倒数第二步，再处理M/E

  • M

IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。以64位浮点数为例，留给M只有52位，将第一位的1舍去以后，等于可以保存53位有效数字。

最后

M = 01

  • E

E为一个无符号整数（unsigned int）。这意味着，如果E为8位，它的取值范围为0~255；如果E为11位，它的取值范围为0~2047。但是，我们知道，科学计数法中的E是可以出现负数的，所以IEEE 754规定，E的真实值必须再减去一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。

最后

E = 1 + 1023 = 1024

5. 最后一步，拼接S/E/M成64位二进制

综上可得

S = 0 => 0
E = 1025 => 100 0000 0000(11位)
M = 01 => 0100 0000 …. 0000(52位)

组合得到

0 100 0000 0000 0100 0000….0000(64位)

和上文用java程序打印出来的结果一致。没有问题 : D

精度丢失举例

有了上面IEEE754例子，那么精度丢失这个问题其实也就迎刃而解了。

0.1(10)其实无法用二进制来精确的表示，使用乘二取整法转成二进制，你会发现是循环的。

在Java中，可通过new BigDecimal(d1).toString()查看实际值。

1
2
3
4
5
6
7
double d = 0.0;
for (int i = 0; i < 10; i++) {
    d = d + 0.1;
    BigDecimal bigDecimal = new BigDecimal(d);
    String s = bigDecimal.toString();
    System.out.println(s);
}

运行结果如下：

1
2
3
4
5
6
7
8
9
10
0.1000000000000000055511151231257827021181583404541015625
0.200000000000000011102230246251565404236316680908203125
0.3000000000000000444089209850062616169452667236328125
0.40000000000000002220446049250313080847263336181640625
0.5
0.59999999999999997779553950749686919152736663818359375
0.6999999999999999555910790149937383830547332763671875
0.79999999999999993338661852249060757458209991455078125
0.899999999999999911182158029987476766109466552734375
0.99999999999999988897769753748434595763683319091796875

当你在java中声明一变量a=0.1时，实际保存的值是0.1000000000000000055511151231257827021181583404541015625。而java展示时，会根据精度四舍五入。

java中的BigDecimal类

为了解决精度丢失的问题，你可以使用BigDecimal,BigDecimal类规避了用二进制存储十进制数据的问题，因为它就是用十进制存储十进制。使用String参数类型的构造函数new BigDecimal(String s)。

BigDecimal序列化的问题

FastJson序列化

参考链接:
https://blog.csdn.net/kisimple/article/details/43773899#commentBox

http://www.ruanyifeng.com/blog/2010/06/ieee_floating-point_representation.html

https://www.wikiwand.com/zh-cn/IEEE_754#/.E8.A7.84.E7.BA.A6.E5.BD.A2.E5.BC.8F.E7.9A.84.E6.B5.AE.E7.82.B9.E6.95.B0

http://hg.openjdk.java.net/jdk7u/jdk7u/jdk/file/70e3553d9d6e/src/share/classes/java/math/BigDecimal.java

Comments

⬆︎TOP