R实现ARIMA预测

ARIMA模型是经典的时间序列预测模型。包含了AR,I,MA三个部分，简单的说，把三个数学公式拼在了一起。具体含义因篇幅原因本文就不展开了。而R语言常在统计领域中出现，可以方便的为统计人员计算并可视化。

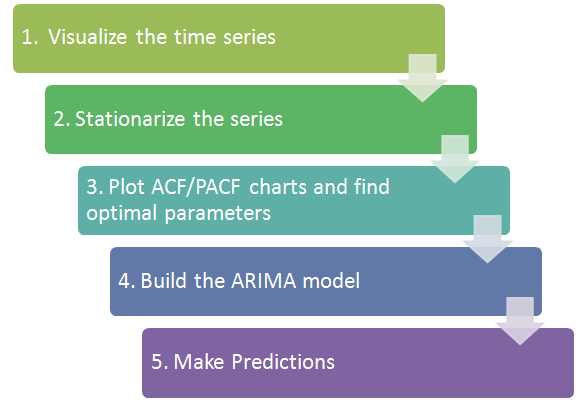
第一次用ARIMA模型，咱们使用R语言内建的AirPassengers数据集，它反映了从1949到1960年的国际航班乘客数量。曲线的特征还是很明显的，我觉得偏于理论学习。下图为ARIMA实现基本步骤。

flowchart.png

  1. 获取数据并可视化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#获取AirPassengers
> data(AirPassengers)
#查看数据的基本信息
> AirPassengers
 Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1949 112 118 132 129 121 135 148 148 136 119 104 118
1950 115 126 141 135 125 149 170 170 158 133 114 140
1951 145 150 178 163 172 178 199 199 184 162 146 166
1952 171 180 193 181 183 218 230 242 209 191 172 194
1953 196 196 236 235 229 243 264 272 237 211 180 201
1954 204 188 235 227 234 264 302 293 259 229 203 229
1955 242 233 267 269 270 315 364 347 312 274 237 278
1956 284 277 317 313 318 374 413 405 355 306 271 306
1957 315 301 356 348 355 422 465 467 404 347 305 336
1958 340 318 362 348 363 435 491 505 404 359 310 337
1959 360 342 406 396 420 472 548 559 463 407 362 405
1960 417 391 419 461 472 535 622 606 508 461 390 432
> start(AirPassengers)
[1] 1949    1
> end(AirPassengers)
[1] 1960   12
> frequency(AirPassengers)
[1] 12
> summary(AirPassengers)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  104.0   180.0   265.5   280.3   360.5   622.0  
```	

接着把获取的数据可视化分析

```R
> plot(AirPassengers)
#增加一条拟合线，lm(应变量~ 自变量)
> abline(lm(AirPassengers ~ time(AirPassengers)))

psgplot

1
2
3
4
#逐年比较，每个月平均值。
> plot(aggregate(AirPassengers,FUN=mean))
#每个月的盒图
> boxplot(AirPassengers~cycle(AirPassengers))

agg
boxplt

得出的结论

  1. 乘客历年增加，不符合平稳过程。
  2. 从盒图中可以发现，每年的7、8月份中位数最大，方差也最大。

  3. 有明显的周期性，周期大致为12。因为历年相同月份的方差不大。

  4. 得到平稳序列

使用ARIMA的前提条件是时间序列是平稳过程，很明显，AirPassengers不是平稳过程。因此，我们得将其转换成平稳过程。消除不平稳性有几个方法：

  • 差分(differencing)
  • 去趋势(detrending)
  • seasonality
  • 取对数log

咱们采取两种方法消除不平稳性：

  1. 对时间序列取对数消除方差的变化，即：让历年同一个月份的方差减小。
1
> plot(log(AirPassengers))

log

  1. 对时间序列取求一阶差分消除趋势。即：让历年的趋势同处于一条水平线。
1
> plot(diff(log(AirPassengers)))

difflog
由于大致可以判断，达到平稳过程的要求。但素，仅凭粗糙的肉眼并不能分辨精确的数学定义。因为这里的数据不复杂，所以问题不大。如果要更进一步区分，我们可以采用Dicky-Fuller检测。若能看分辨出其不稳定，可以再次差分，直到稳定。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 可选，若已安装，可跳过。
> install.packages('tseries')
> install.packages('forecast')
#调用tseries,forecast包
> library('tseries')
> library('forecast') 
#Augmented Dickey-Fuller Test,一般p-value < 0.05则可视为平稳。
> adf.test(diff(log(AirPassengers)),alternative='stationary',k=0)

	Augmented Dickey-Fuller Test

data:  diff(log(AirPassengers))
Dickey-Fuller = -9.6003, Lag order = 0, p-value = 0.01
alternative hypothesis: stationary

Warning message:
In adf.test(diff(log(AirPassengers)), alternative = "stationary",  :
  p-value smaller than printed p-value

由上述的adf测试得出结果，p-value<0.01,拒绝原假设，即序列稳定。

  1. 通过ACF,PACF找到ARIMA最优参数

1
2
> acf(diff(log(AirPassengers)))
> pacf(diff(log(AirPassengers)))

acf
pacf
很明显，ACF图在滞后一阶后，降到蓝线以下，所以q=1,而PACF在滞后0阶滞后降到蓝线一下，因此p为0；加上第二步中的一阶差分，d=1。最后得出模型ARIMA(0,1,1)。

小彩蛋auto.arima()

直接利用R的auto.arima(data,trace=T)选出最优参数可不是轻轻松松(￣▽￣)~*

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
> auto.arima(data,trace=T)

 ARIMA(2,0,2)(1,1,1)[12] with drift         : Inf
 ARIMA(0,0,0)(0,1,0)[12] with drift         : -432.7415
 ARIMA(1,0,0)(1,1,0)[12] with drift         : -472.4967
 ARIMA(0,0,1)(0,1,1)[12] with drift         : -481.1033
 ARIMA(0,0,0)(0,1,0)[12]                    : -434.799
 ARIMA(0,0,1)(1,1,1)[12] with drift         : -479.454
 ARIMA(0,0,1)(0,1,0)[12] with drift         : -447.8018
 ARIMA(0,0,1)(0,1,2)[12] with drift         : -479.5049
 ARIMA(0,0,1)(1,1,2)[12] with drift         : Inf
 ARIMA(1,0,1)(0,1,1)[12] with drift         : -479.4557
 ARIMA(0,0,0)(0,1,1)[12] with drift         : -465.3811
 ARIMA(0,0,2)(0,1,1)[12] with drift         : -479.1627
 ARIMA(1,0,2)(0,1,1)[12] with drift         : Inf
 ARIMA(0,0,1)(0,1,1)[12]                    : -483.204
 ARIMA(0,0,1)(1,1,1)[12]                    : -481.5888
 ARIMA(0,0,1)(0,1,0)[12]                    : -449.8846
 ARIMA(0,0,1)(0,1,2)[12]                    : -481.6381
 ARIMA(0,0,1)(1,1,2)[12]                    : Inf
 ARIMA(1,0,1)(0,1,1)[12]                    : -481.5755
 ARIMA(0,0,0)(0,1,1)[12]                    : -467.459
 ARIMA(0,0,2)(0,1,1)[12]                    : -481.2929
 ARIMA(1,0,2)(0,1,1)[12]                    : -481.5558

 Best model: ARIMA(0,0,1)(0,1,1)[12]                    

Series: data 
ARIMA(0,0,1)(0,1,1)[12] 

Coefficients:
          ma1     sma1
      -0.4018  -0.5569
s.e.   0.0896   0.0731

sigma^2 estimated as 0.001369:  log likelihood=244.7
AIC=-483.39   AICc=-483.2   BIC=-474.77

  1. 建立ARIMA模型并预测

预测五年后乘客的数量趋势：

1
2
3
> fit <- arima(log(AirPassengers), c(0, 1, 1),seasonal = list(order = c(0, 1, 1), period = 12))
> pred <- predict(fit, n.ahead = 5*12)
> ts.plot(AirPassengers,2.718^pred$pred, log = "y", lty = c(1,3))

predict

  1. 预测模型检验

利用LBQ test检验模型是否合格，也就是检验残差是否为白噪声。

Comments

⬆︎TOP