左倾红黑树

阅读完《算法》(第4版)的查找部分，初步了解了左倾红黑树的原理和部分实现,包括树的建立、删除最大节点和删除最小节点。这里默认你掌握了BST和2-3-4树的基本操作。

左倾红黑树的渊源

我们都知道，对于BST来说，最致命的缺点莫过于，当插入的键有序时，BST的树高是线性增长的，此时他的get(),put()操作的时间复杂度都是N，为了解决这个问题，就有了AVL（平衡二叉树，不在此篇讨论范围）的平衡操作（左旋，右旋）来保证树左右子树的平衡。那么，明明AVL看上去已经完美的结构，为什么还会冒出红黑树呢？因为，AVL也还是有缺点：插入时太多的平衡操作也会影响插入时的性能。我只是定性的提了提，定量的分析可以参考其他文献资料。而红黑树的插入操作所带来的平衡操作相对更少，从而更加高性能的插入，但是带来的负面结果便是树的高度有所增加：叶子节点到根节点的最长路径<=2*叶子节点到根节点的最短路径。可以说红黑树是更加折策略中的结果。

在《算法》（第4版）中，红黑树的实现直接采用了左倾红黑树的方法，左倾红黑树可以用更少的代码量实现红黑树，我也便使用他的方法理解。

2-3-4树和左倾红黑树的等价转换

我们把树中的链分为3种类型：

  1. 红链接连接两个2-节点构成一个3-节点

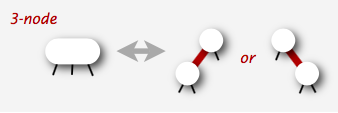
  2. 黑链接则是2-3树中的普通连接。

  3. 第三种，类型会临时出现，稳定的2-3树不会出现，2-3-4中会出现，它是4-节点

    这么一来，我们便可以用一棵BST来代表2-3-4树了。

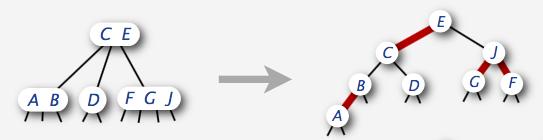
    但是有个问题，对于三节点的表示，有两种表示方法，一种是红链左倾，另一种是红链右倾，所以要考虑很多种情况，但是我们只考虑左倾的情况，也就是对于3-节点，我们只有下图一种转换关系：

    构成的树也称左倾红黑树（Left-Leaning Red-Black Trees）,如下图：

不允许出现的情况

  • 右倾的3-节点

  • 两个红链接首尾相连

Java左倾红黑树的数据结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class BST<Key extends Comparable<Key>, Value>
{ 
private static final boolean RED   = true;
private static final boolean BLACK = false;
private Node root;
private class Node
{
    Key key;
    Value val;
    Node left, right;
    boolean color;
    Node(Key key, Value val, boolean color)
    {
        this.key   = key;
        this.val = val;
        this.color = color;
	}	
} 
   public Value get(Key key)
   // Search method.
   public void put(Key key, Value val)
   // Insert method.
   public void delMax(Key key)
}
private boolean isRed(Node x)
{
	if (x == null)
		return false;
	return (x.color == RED);
}

除了红黑树的put(),delete(),delMax(),delMin()这些涉及到节点颜色的操作之外，如get(),rank
(),max(),min(),floor(),ceiling()都是和BST一样的，一行都不用改，原因是红黑树本质上是一棵BST，所以说红黑树的确是个伟大的发明👍。

红黑树的插入

红黑树的插入是一个比较复杂的操作，使用递归实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
private Node put(Node x, Key key, Value val){
    // 从Node x 开始put
    // 如果存在key,在更新key所在节点的val
    // 否则新建一个叶子节点
    if (x == null) return new Node(key,val,1);
    int cmp = key.compareTo(x.key);
    if (cmp < 0){
        return put(x.left,key,val);
    }
    else if (cmp > 0){
        return put(x.right,key,val);
    }
    else{
        x.val = val;
    }
    // 更新子树的节点个数
    x.N = x.left.N + x.right.N + 1;
    return x;
}

平衡红黑树操作

在红黑树中只需要维护黑链接的平衡，只需要对红色的链接进行旋转操作，这俩是基本的工具方法，很多地方都要用到，所以封装成两个私有的内部方法。

1
2
3
4
5
6
7
8
9
10
11
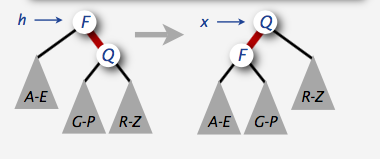
12
private Node rotateLeft(Node h){
    // 向左旋转
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    x.color = h.color;
    h.color = RED;
    // 更新节点计数器 todo 此处略有不熟
    x.N = h.N;
    h.N = 1 + size(h.left) + size(h.right);
    return x;
}


1
2
3
4
5
6
7
8
9
10
11
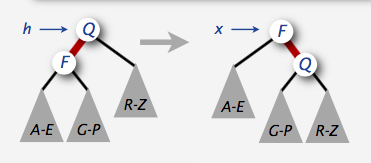
12
private Node rotateRight(Node h){
    // 向右旋转,与向左相反
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    x.color = h.color;
    h.color = RED;
    // 更新节点计数器 todo 此处略有不熟
    x.N = h.N;
    h.N = 1 + size(h.left) + size(h.right);
    return x;
}

在LLRBtree底部插入一个新的节点

  1. 把添加的新节点的color设为红色。
  2. 如果有必要的话，执行旋转操作。其中的有必要是指哪些情况呢？就是上文不允许出现的情况。转换关系如下图：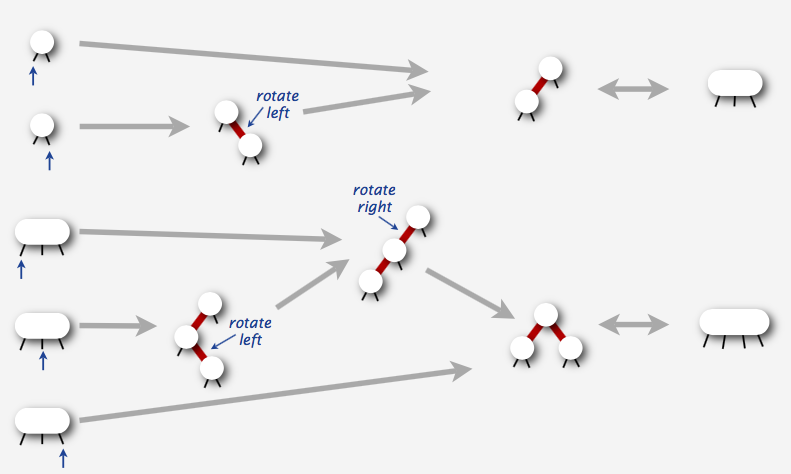

把4-节点分解

这个很好实现，把两个子节点的颜色改为黑，父节点的颜色改成红色即可。

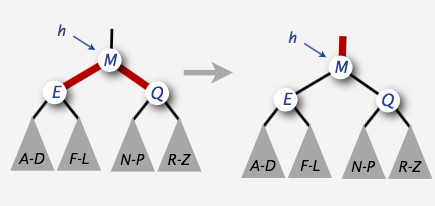
书上的实现是这样的：

1
2
3
4
5
private void flipColors(Node h){
    h.left.color = BLACK;
    h.right.color = BLACK;
    h.color = RED;
}

但是论文上的实现更加统一，也避免了再添加一个逆操作函数(在删除节点操作中，子节点颜色改为红，父节点颜色改为黑),

1
2
3
4
5
6
7
private Node colorFlip(Node h)
{
	x.color = !x.color;
	x.left.color = !x.left.color;
	x.right.color = !x.right.color;
	return x;
}

在LLRB中分解4-节点

  1. 分解4-节点,红链接会上升一个level
  2. 如果有必要，则rotate。
  • 当父节点是2-节点时
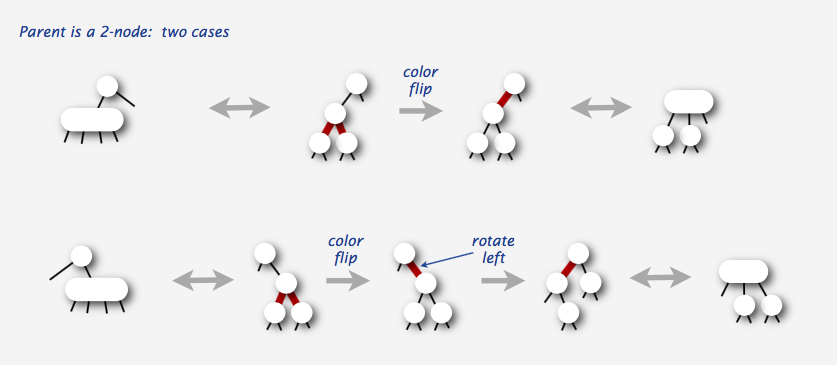
  • 当父节点是3-节点时

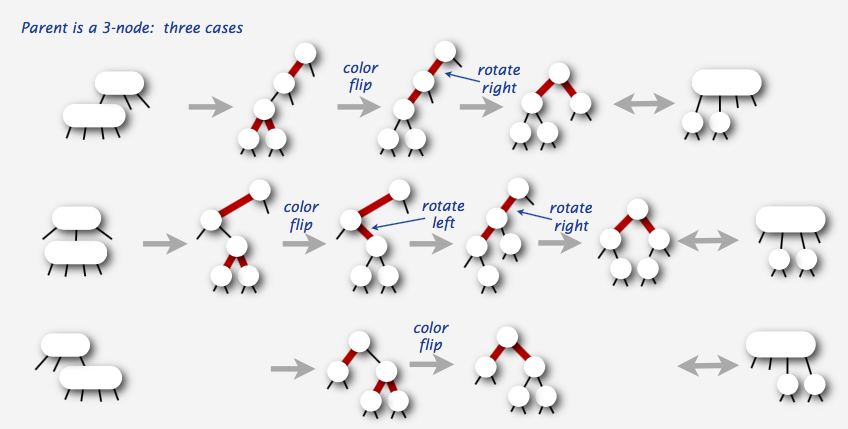
LLRT的插入算法


这里代码的执行顺序是很重要的。
比如如果我们把colorfilp移到最后，那么会出现什么情况？
由于每次在最后都将4-node 进行color flip了，那么自然红黑树中不存在4-node了，所以就变成了2-3树的红黑树，这也是书本上的结果。

LLBT节点的删除

删除最大节点

参考链接：

https://blog.csdn.net/bytxl/article/details/40920165
http://www.cs.princeton.edu/~rs/talks/LLRB/RedBlack.pdf
https://cloud.tencent.com/developer/article/1193097

Comments

⬆︎TOP